¿Qué es la razón de dos segmentos?

Para entender el teorema de Tales es necesario que entiendas muy bien qué es la razón entre dos segmentos.

Por ejemplo, tenemos estos dos segmentos:

Como ya sabes, los segmentos están delimitados por dos extremos y se nombran por los extremos que lo limitan. Al segmento rojo, que empieza en el extremo A y termina en el extremo B, se le llama segmento AB.

Si dos segmentos tienen alguna relación entre ellos, se utilizan las mismas letras para nombrarlos, pero como no pueden repetirse, se utiliza la comilla simple al lado de cada letra y esa comilla se lee “prima”. Por tanto A’, se leería “A prima”.

Así pues, al segmento azul, que empieza en A’ y termina en B’, lo llamaremos segmento A’B’.

La razón (o relación) de dos segmentos es el resultado de dividir la longitud de esos dos segmentos.

Si el segmento AB mide 5 cm y el segmento A’B’ mide 10 cm, ¿cuál la razón de estos dos segmentos?

Sólo tenemos que dividir la longitud del segmento AB entre la longitud del segmento A’B’:

La razón de esos dos segmentos es 0,5, que significa que AB es la mitad que A’B’.

También podemos calcular la razón dividiendo la longitud del segmento A’B’ entre la longitud del segmento AB:

En este caso, la razón es 2, o con otras palabras, el segmento A’B’ es el doble que el segmento AB.

Si te das cuenta, decir que el segmento AB es la mitad que el segmento A’B’, es lo mismo que decir que el segmento A’B’ es el doble que el segmento AB.

Por tanto, para calcular la razón no es necesario hacerlo de ambas formas. Calculándola por una de las dos formas es suficiente.

Proporcionalidad entre pares de segmentos

Tenemos ahora estos dos segmentos:

El segmento rojo, CD, mide 3 cm y el segmento azul C’D’ mide 6 cm.

Vamos a calcular su razón:

La razón de los segmentos CD y C’D’ es la misma que la razón de los segmentos AB y A’B’.

Cuando dos pares de segmentos tienen la misma razón, se dice que son proporcionales.

Por tanto los segmentos AB y A’B’ son proporcionales a CD y C’D’:

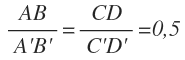
Dos pares de segmentos son proporcionales cuando su razón es la misma.

El teorema de Tales

Una vez que te he explicado la razón entre dos segmentos y la proporcionalidad entre dos pares de segmentos, vamos a ver el teorema de Tales.

Tenemos dos rectas secantes (que no son paralelas). A una la llamaremos la recta r (color rojo) y a la otra la llamaremos la recta s (color azul):

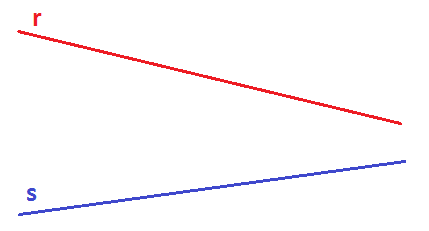
A estas dos rectas, las cortamos con varias rectas paralelas (color verde), de la siguiente manera:

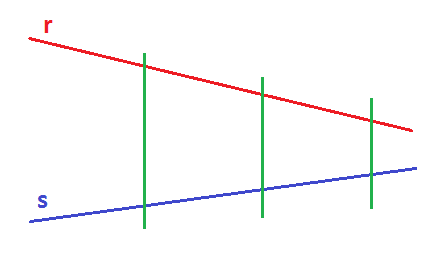
A los puntos donde cortan las rectas paralelas a la recta r, los voy a llamar A, B y C y a los puntos donde cortan las rectas paralelas a la recta s, los llamaré A’, B’ y C’:

Las rectas verdes, han dividido a la recta r en dos segmentos: el segmento AB y el segmento BC. Además tenemos un tercer segmento si consideramos la primera y la última recta paralela, es decir, el segmento AC.

También han dividido a la recta s en dos segmentos A’B’ y B’C’ y si consideramos la primera y la última recta paralela, existe un tercer segmento A’C’.

El teorema de Tales nos dice lo siguiente:

¿Y eso qué quiere decir?

Pues que si divides las longitudes de los segmentos que están enfrentados, es decir, el segmento AB entre el segmento A’B’ tienen la misma razón que si divides el segmento BC entre el segmento B’C’:

Como tienen la misma razón, AB y A’B’ son proporcionales a BC y B’C’.

Si consideramos el segmento formado por la primera y la última recta paralela, es decir, el segmento AC, también es proporcional al segmento AB:

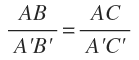
Y por tanto, todos los segmentos de la recta r son proporcionales a los segmentos de la recta s:

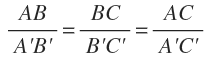
¿Para qué sirve el teorema de Tales?

El teorema de Tales te permite calcular la longitud de un segmento, conocidos los valores de todos los demás segmentos de dos rectas que se encuentran en posición de Tales.

Encontrarse en posición de Tales significa que las rectas tienen que estar tal y como dice el teorema de Tales, es decir, dos rectas secantes cortadas por varias rectas paralelas.

Vamos a resolver varios ejercicios para que te quede mucho más claro.

Ejercicios resueltos del teorema de Tales

Ejercicio 1

Las rectas a y b del dibujo son paralelas. Comprueba utilizando el teorema de Tales si también lo es la recta c.

¿Cómo demostramos que la recta c es paralela?

Pues tenemos que demostrar que las rectas están en posición de Tales y que se cumple el teorema de Tales, comprobando si los segmentos de ambas rectas tienen la misma razón y que entre ellas sean proporcionales.

Calculamos la razón de los primeros segmentos:

Y la razón de los siguientes dos segmentos:

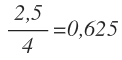
La razón es la misma, por lo que ambos pares de segmentos son proporcionales.

Entonces se cumple el teorema de Tales y como consecuencia, la recta c es paralela.

Ejercicio 2

¿Cuánto mide el segmento x en este dibujo?

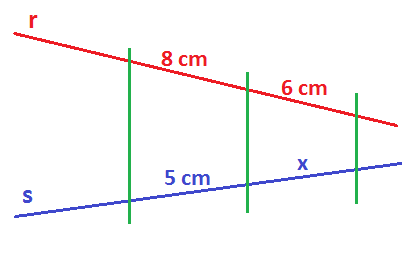
Sabemos lo que miden los dos segmentos de r, pero falta por saber cuánto mide uno de los segmentos de s, por lo que a ese segmento le llamamos x.

Entonces, según el teorema de Tales, los tramos que están enfrentados tienen la misma razón, por lo que sus divisiones deben de dar lo mismo y por tanto las podemos igualar:

Nos queda una ecuación de primer grado, de donde tenemos que despejar la x.

Hay mucha confusión para resolver ecuaciones de este tipo. (Si quieres aprender mucho más sobre cómo resolver ecuaciones de primer grado, te recomiendo el Curso de Ecuaciones de Primer Grado)

Para resolver esta ecuación, pasamos los denominadores de cada miembro, multiplicando al numerador del miembro contrario (multiplicamos en cruz).

El 5 que está dividiendo al 8 en el primer miembro, pasa multiplicando al 6 del segundo miembro y la x, que está dividiendo al 6 en el segundo miembro, pasa multiplicando al 8 en el primer miembro y nos queda así:

Ya no tenemos denominadores. Vamos a despejar la x.

Ahora, el 8 que está multiplicando a la x, pasa al segundo miembro dividiendo:

Y finalmente operamos para calcular el valor de x:

Que si lo compruebas, los pares de segmentos serán proporcionales.